1. 그래프(Graph)
- 연결되어 있는 객체 간의 관계를 표현하는 자료 구조
- 그래프는 정점(Vertex)과 이들을 연결하는 간선(Edge)들의 집합으로 구성된다.
- N:N 관계 표현이 용이하다.
✔️ 종류
: 간선(edge)의 종류에 따라 구분
- 무향 그래프 (Undirected Graph)
- 양 방향으로 이동
- ex) (A,B) (B,A)
- 유향 그래프 (Directed Graph)
- 간선의 방향으로만 이동 가능
- ex) <A,B>
- 가중치 그래프 (Weighted Graph)
- 간선에 비용(cost) 또는 가중치(weight)가 할당된 그래프
- ex) 네트워크
- 사이클 (Cycle)
- 시작 정점과 종료 정점이 동일한 그래프
- 비순환 그래프 (Acyclic Graph)
- 사이클이 없는 그래프
- 완전 그래프 (Complete Graph)
- 그래프에 속해 있는 모든 정점이 서로 연결되어 있는 그래프
- 그래프에 속해 있는 모든 정점이 서로 연결되어 있는 그래프
2. 그래프 구현
그래프를 구현할 때 간선을 어떻게 저장할 건지는 메모리, 성능을 고려해서 정해야 한다.
1) 인접 리스트 (Adjacency List)
각 정점에 인접한 정점들을 연결 리스트로 저장하는 것이다.

✔️ 공간복잡도 (메모리)
간선의 개수를 알고 있기 때문에 필요한 만큼의 메모리 공간을 사용한다.
따라서 메모리를 효율적으로 사용한다.
✔️ 시간 복잡도
- 특정 두 정점 간의 연결 여부 탐색할 때 느리다.
2) 인접 행렬 (Adjacency Matrix)
# 연결되어 있을 때
graph[i][j] = 1;
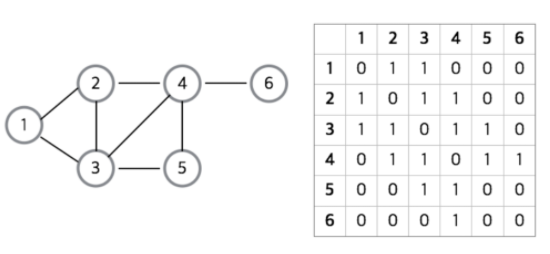
행렬로 표현하는 경우에는 인덱스가 정점이 된다.
그래서 예를 들어, graph[1][2] = 1 인 경우에는 1번 노드 -> 2번 노드로 연결되어 있다는 의미이다.
만약 방향성이 없는 그래프라면 graph[1][2]= 1, graph[2][1]= 1가 된다.
✔️ 공간복잡도 (메모리)
간선 수와 무관하게 n^2 메모리 공간을 사용한다.
✔️ 시간 복잡도
- 특정 두 정점 간의 연결 여부. 즉, 간선 존재 여부를 확인할 때는 O(1)로 알 수 있다.
- 특정 노드의 인접한 모든 노드를 알기 위해서는 전부 순회해야 한다.
- 모든 간선 수 계산은 전부 순회해야 한다. O(N^2).
📌 Reference
반응형
'Computer Science > CS' 카테고리의 다른 글
| [자료구조] 서로소 집합 (Disjoint Sets), 사이클 판별 알고리즘 (1) | 2022.08.08 |
|---|---|
| [알고리즘] 그래프 탐색 알고리즘 DFS / BFS (0) | 2022.08.03 |
| [자료구조] 트리 (Tree) (0) | 2022.07.29 |
| [자료구조] 연결 리스트 (Linked list) (0) | 2022.07.27 |




댓글