[ 이진 탐색 트리(BST, Binary Search Tree)의 단점 ]
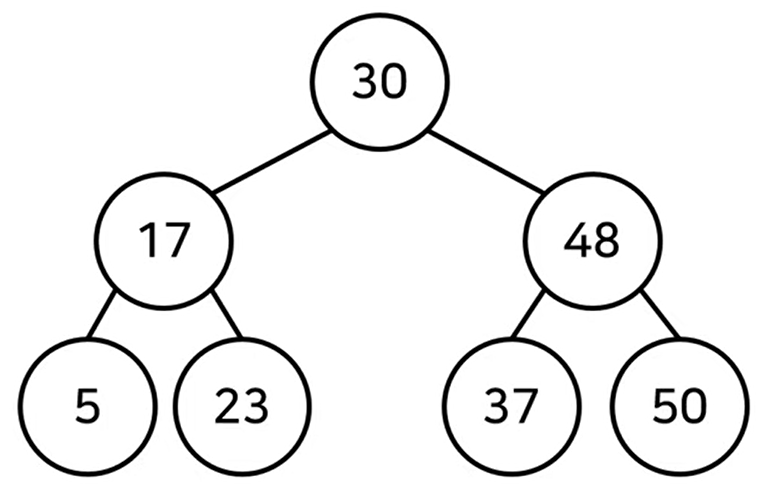
균등 트리 : 노드 개수가 N개일 때 O(logN)
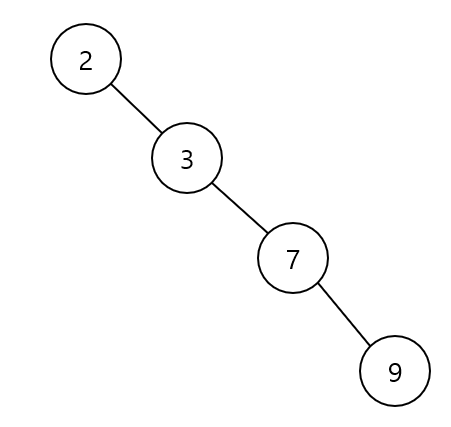
편향 트리 : 노드 개수가 N개일 때 O(N)
이진 탐색 트리는 최악의 경우 한쪽으로 편향된 트리일 때 O(N) 시간이 걸린다.
이 말은 모든 노드를 한 번씩 다 확인해줘야 한다는 의미이다.
이러한 단점을 개선한 균형 트리인 Red-Black 트리에 대해서 알아보자.
🔴 Red-Black 트리 ⚫️
이진 탐색 트리의 단점을 개선하기 위한 자료구조
- 이진 탐색 트리(BST)의 한 종류
- 스스로 균형(balancing) 잡는 트리
- BST의 worst case의 단점을 개선해서 모든 경우에 O(logN)
- 모든 노드는 red 혹은 black

✔️ 5가지 속성
- 모든 노드는 red 혹은 black
- 루트 노드는 black
- 모든 nil(leaf) 노드는 black
- red의 자녀들은 반드시 black이어야 한다. (즉, red가 연속적으로 존재할 수 없다.)
- 임의의 노드에서 자손 nil 노드들까지 가는 경로들의 black 수는 같다. (자기 자신은 카운트에서 제외)
- 8번 노드를 예로 들어보자.
- 8번 노드에서 자손 nil 노드들까지 가는 경로는 5가지이다.
- 각각의 경로 모두 black의 수가 2개로 동일하다.
[ nil 노드란? ]
- 존재하지 않음을 의미하는 노드
- 자녀가 없을 때 자녀를 nil 노드로 표기
- 값이 있는 노드와 동등하게 취급
- RB 트리에서 leaf 노드는 nil 노드
[ 노드 x의 black height ]
#5 속성: 임의의 노드에서 자손 nil 노드들까지 가는 경로들의 black 수는 같다. (자기 자신은 카운트에서 제외)
- 노드 x에서 임의의 자손 nil 노드까지 내려가는 경로에서의 black 수 (자기 자신은 카운트에서 제외)
- 위의 속성 중 5번을 만족해야 성립하는 개념이다.
[ 예시 ]
위의 그림을 다시 가져와 살펴보자.

- 노드 8의 black height : 2
- 노드 13의 black height : 2
✔️ Red-Black 트리는 어떻게 균형을 잡을까?
#4 속성: red의 자녀들은 반드시 black이어야 한다. (즉, red가 연속적으로 존재할 수 없다.)
#5 속성: 임의의 노드에서 자손 nil 노드들까지 가는 경로들의 black 수는 같다. (자기 자신은 카운트에서 제외)
삽입/삭제 시 주로 속성 #4, #5를 위반하며 이들을 해결하기 위해 구조를 바꾼다.
그러다 보면 자연스럽게 트리의 균형이 잡히게 된다.
이렇게 균형을 잡으며 편향되지 않는다.
✔️ 삽입 동작 방식
전체 큰 그림으로 우선 살펴보자.
삽입 전 RB 트리 속성 만족한 상태
삽입 방식은 일반적인 BST와 동일
삽입 후 RB 트리 위반 여부 확인
RB 트리 속성을 위반했다면 재조정
RB 트리 속성을 다시 만족BST와 동일하게 삽입하고 트리 속성을 만족하도록 조정한다.
삽입하는 노드는 항상 red다.
[ 예시 ]
1. insert(50)
- 삽입하는 노드는 항상 red다.
- 삽입 시 nil 노드의 색은 black으로 고정한다.
- #3 속성 만족
- 모든 nil(leaf) 노드는 black
- #2 속성 위반
- 루트 노드는 black
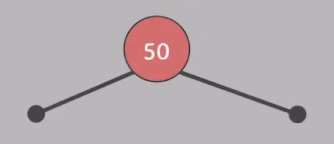
- 루트 노드를 red에서 black으로 바꿔준다.
- 모든 속성 만족

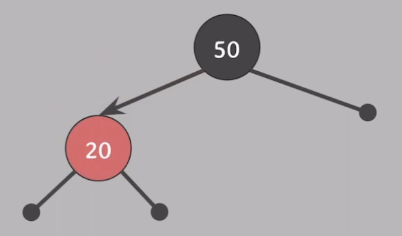
2. insert(20)
- 삽입하는 노드는 항상 red다.
- 모든 속성 만족
🧐❓ 왜 새로 삽입하는 노드는 red일까?
🙋♀️💡 삽입한 후에도 #5 속성을 만족하기 위해서
#5 속성: 임의의 노드에서 자손 nil 노드들까지 가는 경로들의 black 수는 같다. (자기 자신은 카운트에서 제외)
3-1. insert(10)
- 삽입하는 노드는 항상 red다.
- #4 속성 위반
- red의 자녀들은 반드시 black이어야 한다. (즉, red가 연속적으로 존재할 수 없다.)
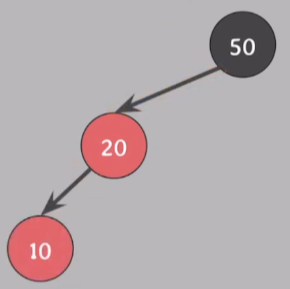
🧐❓이 상황은 어떻게 해결할 수 있을까?
🧐 red가 한 쪽으로 몰려 있으니 red 하나를 반대편으로 옮겨준다면?
🧐 구조를 바꿔준 뒤에도 BST의 특징 또한 유지되어야 한다!
🙋♀️💡 그 방법은 🌀회전🌀이다!!
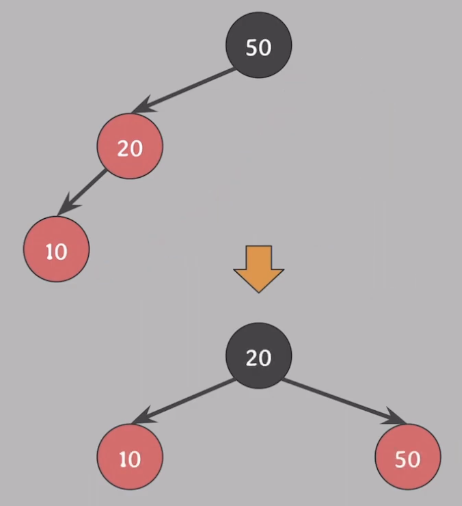
- #4 속성 위반을 해결하기 위해 red 하나를 옮겨야 함.
- BST 특징 또한 유지하면서 넘기기 위해 회전을 사용한다.
- 20과 50의 색을 바꿔준다.
- 50을 기준으로 오른쪽으로 회전한다.
- 모든 속성 만족
3-2. insert(40)
2번 상황에서 또 다른 삽입 경우를 살펴보자.
- 삽입하는 노드는 항상 red다.
- #4 속성 위반
- red의 자녀들은 반드시 black이어야 한다. (즉, red가 연속적으로 존재할 수 없다.)
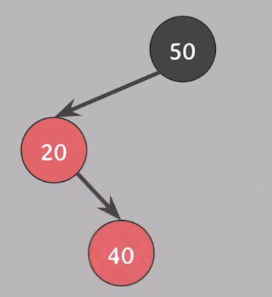
- 위의 3번 케이스(insert(10))와 다른 점은 루트 노트까지 경로가 꺾여있다.
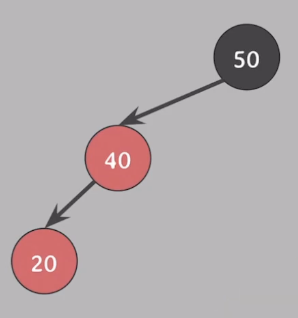
- 회전
- 20 기준으로 왼쪽으로 회전한다.
- 그다음 위의 케이스와 동일하게 회전해 준다.
- 모든 속성 만족
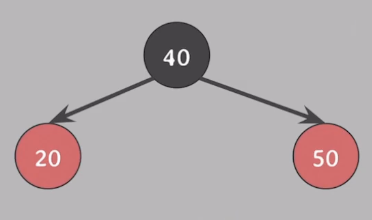
4. insert(30)
3-1번 상황에서 30을 삽입한 경우를 살펴보자.
- 삽입하는 노드는 항상 red다.
- #4 속성 위반
- red의 자녀들은 반드시 black이어야 한다. (즉, red가 연속적으로 존재할 수 없다.)
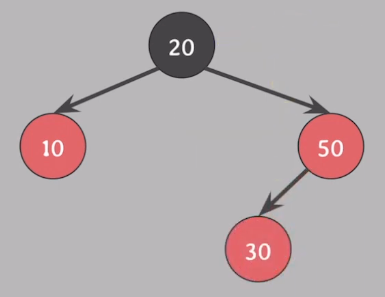
- 지난 케이스와 다르게 red가 한쪽으로 몰려있지 않아 노드를 옮길 수가 없다.
- 또한 #5 속성을 위반하지 않고 조정해줘야 한다.
- 자녀의 색상이 같으면 부모와 자녀의 색상을 서로 바꿔줘도 #5 속성을 위반하지 않는다는 특징이 있다.
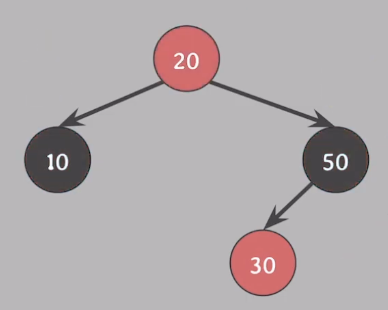
- 10,50 그리고 20의 색상을 바꿔준다.
- #2 속성 위반
- 루트 노드는 black
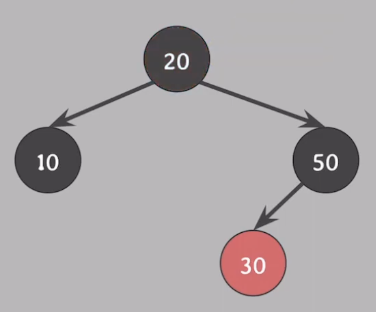
- 20을 black으로 바꿔준다.
- 모든 속성 만족
[ 퀴즈 ]
위의 내용을 바탕으로 이 상황에서 삽입을 하면 어떻게 될지 생각해 보자! (숙제!)
- insert(40)
- insert(35)
- insert(25)
✔️ 삭제 동작 방식
전체 큰 그림으로 우선 살펴보자.
0. 삭제 전 RB 트리 속성 만족한 상태
1. 삭제 방식은 일반적인 BST와 동일
2. 삭제 후 RB 트리 속성 위반 여부 확인
3. RB 트리 속성을 위반했다면 재조정
4. RB 트리 속성을 다시 만족
[ 삭제 후 RB 트리 속성 위반 여부 확인 ]
💡 삭제되는 색을 통해 속성 위반 여부를 확인한다.
🧐❓삭제되는 색이 뭔데?
💡 삭제하려는 노드의 자녀가 없거나 하나라면 삭제되는 색은 삭제되는 노드의 색
💡 삭제하려는 노드의 자녀가 둘이라면 삭제되는 색은 삭제되는 노드의 successor의 색
🧐❓그게 무슨 소린데?
예시로 살펴보자!
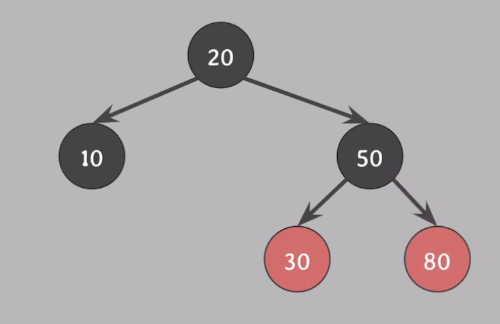
[ 예시 1 ]
삭제하려는 노드의 자녀가 없거나 하나일 때
삭제되는 색은 삭제되는 노드의 색
1) 25를 삭제하면 red 삭제
2) 40을 삭제하면 black 삭제
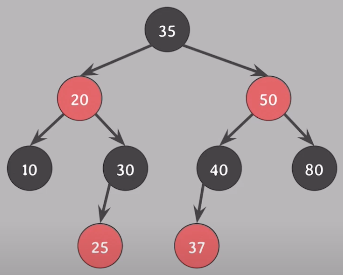
[ 예시 2 ]
삭제하려는 노드의 자녀가 둘일 때
위 그림 그대로 살펴보자.
삭제되는 색은 삭제되는 노드의 successor의 색
1) 20을 삭제하면 successor 25가 20의 자리로 올라오고 색은 20을 이어받는다. 이때는 삭제되는 색은 25의 red이다.
* successor은 오른쪽 서브트리의 가장 작은 값을 가지는 노드이다.
2) 50을 삭제하면 successor 80이 50의 자리로 올라오고 색은 red를 이어받는다. 이때 삭제되는 색은 80의 black이다.
삭제되는 색이 어떤 건지 알아봤다.
이제 이것으로 속성을 위반하는지 알아보자.
1) 삭제되는 색이 red일 때
💡 어떠한 속성도 위반하지 않는다!!
속성 5가지
모든 노드는 red 혹은 black
루트 노드는 black
모든 nil(leaf) 노드는 black
red의 자녀들은 반드시 black이어야 한다. (즉, red가 연속적으로 존재할 수 없다.)
임의의 노드에서 자손 nil 노드들까지 가는 경로들의 black 수는 같다. (자기 자신은 카운트에서 제외)
하나씩 살펴보자.
#1 : 당연히 만족
#2, #3 : 삭제되는 색이 red기 때문에 루트노드나 nil 노드가 삭제되는 것은 아니다.
#4 : 이것 역시 red가 삭제된 것이기 때문에 위반되지 않는다.
#5 : red가 삭제되었기 때문에 black 수에는 영향 X
2) 삭제되는 색이 black일 때
💡 #2, #4, #5 속성 위반할 수 있다.
40을 삭제했다. 40의 자녀가 하나이기 때문에 삭제된 색은 black이다.
#4 : red가 연속되기 때문에 위반한다.
#5 : 모든 경로의 black가 같지 않다. 50에서 왼쪽을 타고 가면 black이 하나이고, 오른쪽으로 가면 2개이다. (nil노드 포함)
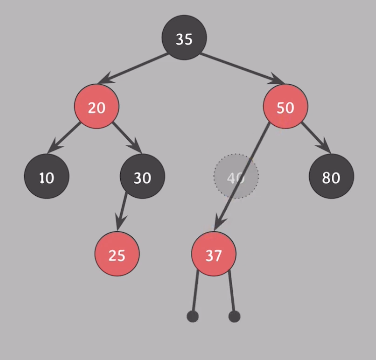
이번에는 아래 상황에서 35를 삭제한다. 자녀가 하나이기 때문에 삭제된 색은 black이다.
#2 : 35가 삭제되고 50이 루트노드가 된다. 그러면 루트 노드가 red로 속성을 위반한다.
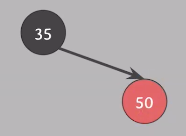
지금까지 위반여부를 확인하는 2번 과정까지 살펴봤다.
이제 위반된 경우 재조정하는 과정을 살펴보자!
[ RB 트리 속성을 위반했다면 재조정 ]
#2를 위반하는 경우 같은 단순한 상황에서는 50을 black으로 바꾸면 된다.
그런데 보통의 경우는 항상 #5를 위반하게 된다. (black을 삭제했기 때문)
이럴 때 해결하는 방식의 red-black tree의 핵심이다!
💡 extra black 부여
#5 속성을 다시 만족시키기 위해 삭제된 색의 위치를 대체한 노드에 extra black을 부여한다.
[ 예시 ]
1) 10 삭제, 삭제되는 색은 black
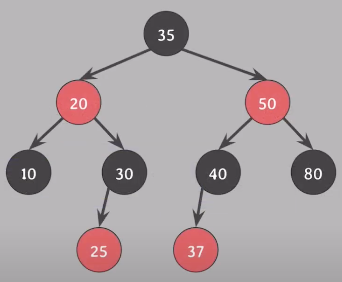
2) #5 속성 위반
3) 삭제된 10의 위치를 대체한 nil 노드에 extra black 부여
4) #5 속성 만족
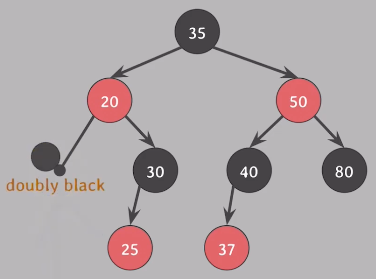
* doubly black : extra black이 부여된 black 노드
* red-and-black : extra black이 부여된 red 노드
💡 red-and-black이 되면 black으로 바꿔주면 끝!
💡 doubly black이 되면 case1, 2, 3, 4 중에서 해결하면 된다.
[ case 4 ]
doubly black의 오른쪽 형제가 black & 그 형제의 오른쪽 자녀가 red일 때
👉 그 red를 doubly black 위로 옮기고 옮긴 red로 extra black을 전달해서 red-and-black으로 만들면 red-and-black을 black으로 바꿔서 해결
쉽게 말하라옹!
👉 오른쪽 형제는 부모의 색으로, 오른쪽 형제의 오른쪽 자녀는 black으로, 부모는 black으로 바꾼 후에 부모를 기준으로 왼쪽으로 회전하면 해결
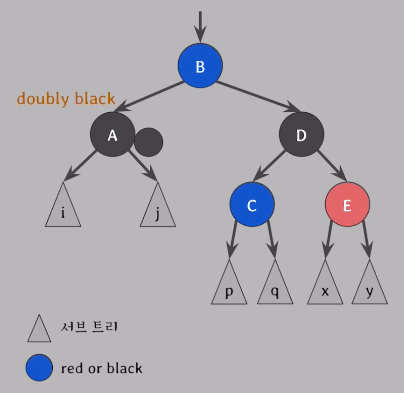

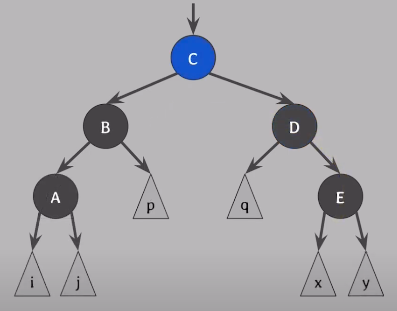
[ case 3 ]
doubly black의 오른쪽 형제가 black & 그 형제의 왼쪽 자녀가 red & 그 형제의 오른쪽 자녀는 black일 때
👉 doubly black의 형제의 오른쪽 자녀가 red가 되게 만들어서 이후엔 case4를 적용하여 해결
👉 E 위치에 red가 오도록 만들기 위해 C와 D의 색을 바꾼 후에 D를 기준으로 오른쪽으로 회전하면 된다.
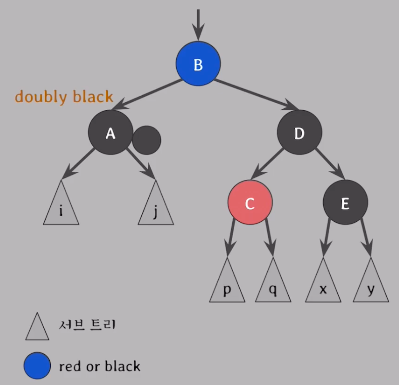
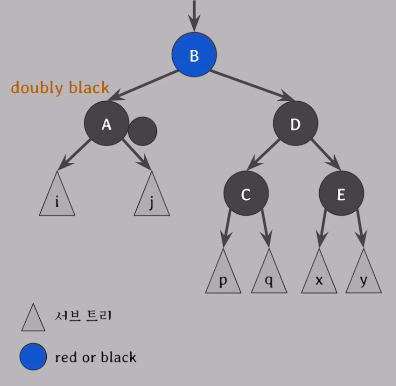
[ case 2 ]
doubly black의 형제가 black & 그 형제의 두 자녀 모두 black일 때
👉 doubly black과 그 형제의 black을 모아서 부모에게 전달해서 부모가 extra black을 해결하도록 위임한다.
[ case 1 ]
doubly black의 형제가 red일 때
👉 doubly black의 형제를 black으로 만든 후 case 2, 3, 4 중 하나로 해결
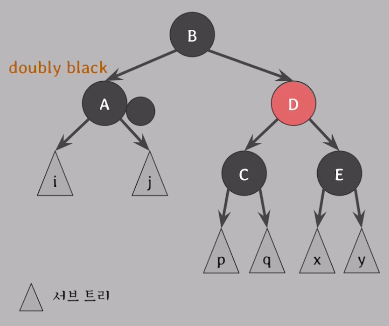
D를 black으로 만들기 위해서 B와 D 색상을 바꿔준다. 그리고 B를 기준으로 왼쪽으로 회전한다.
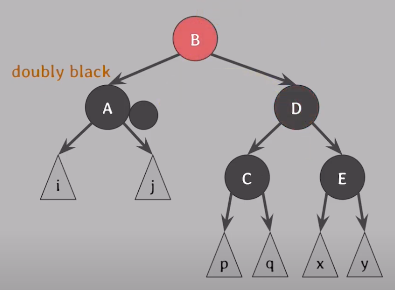
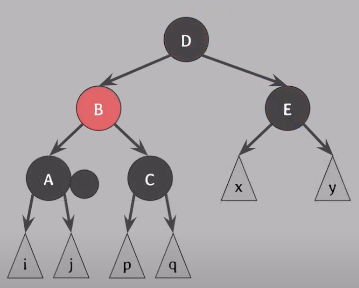
이 상태에서 다른 case 중에서 해결
✔️ 시간 복잡도
N = 트리의 노드 수
| avg | worst | |
| insert | O(logN) | O(logN) |
| delete | O(logN) | O(logN) |
| search | O(logN) | O(logN) |
AVL 트리와 비교했을 때!
- 삽입/삭제가 거의 없고 검색이 대부분인 상황에서는 AVL트리를 사용하고 삽입/삭제가 많을 때는 red-black tree를 사용하면 좋다.
- 왜냐하면 AVL트리는 검색 성능이 빠르고 red-black tree는 삽입/삭제 성능이 좋기 때문!
- AVL트리는 균형을 좀 더 엄격하게 잡는다. 엄격하니깐 검색 성능은 더 좋지만 삽입/삭제는 red-black tree에 비해 느리다.
red-black tree의 응용사례
- linux kernel 내부에서 사용
- Java에서 TreeMap 구현에도 사용된다.
'Computer Science > CS' 카테고리의 다른 글
| [알고리즘] 최소 공통 조상(LCA) 알고리즘 (0) | 2023.12.10 |
|---|---|
| [자료구조] hashing, hash function, map, hash table, hash set | 종합 선물 세트..? (2) | 2023.04.18 |
| [알고리즘] 최단 경로 알고리즘 (다익스트라, 플로이드 워셜) (0) | 2022.10.25 |
| [자료구조] 서로소 집합 (Disjoint Sets), 사이클 판별 알고리즘 (0) | 2022.08.08 |




댓글